¿Estudiar cálculo? ¡Debes aprender mejor la integración!

Leer el artículo le ayudará a dominar el arte de la integración, que es una técnica de cálculo importante.

Por: Kenia Meza

En el siguiente artículo aprenderemos qué es la integración y cómo dominar esta técnica matemática. Con eso, también te ayudaremos a saber cómo puedes obtener cálculos instantáneos para cualquier tipo de problema de integración en línea con una calculadora integral. Sí, esta herramienta en línea es una elección perfecta para alguien que busca una solución precisa y paso a paso para la integración.

Con esta herramienta, nunca tendrás problemas de integración. Todo lo cubierto en esta técnica matemática se puede estudiar mejor utilizando la calculadora de integración. Por eso nunca debes ignorar su importancia.

Volviendo al punto de discusión ahora, ¡analicemos la integración en detalle!

¿Qué es la integración?

En matemáticas:

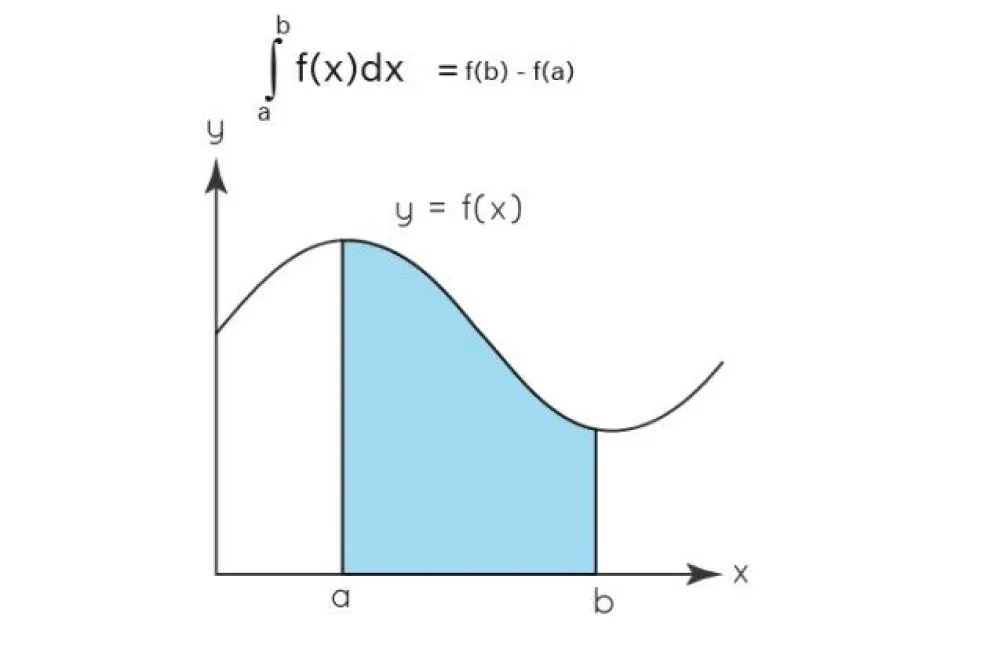
“La integración de una función es un proceso recíproco de diferenciación. Ayuda a encontrar el área debajo de la gráfica determinando la solución a la integral puesta en la función”.

Tipos de Integración:

Normalmente, hay dos tipos de integrales que debes conocer como matemático. Éstas incluyen:

Integral definida:

Esta integral define el área que se acumula bajo el gráfico.

Matemáticamente:

∫(de a a b)

Dónde

a = límite inferior

b = límite superior

Integral indefinida:

Este tipo de integral no tiene límites ni cotas específicas. Se denota con el símbolo “∫”.

En una integral indefinida siempre hay una constante que ayuda a completar el efecto de la integración cuya derivada vuelve a ser la función original sobre la que se aplicó la integración al inicio.

Fórmulas de Integración:

Si es nuevo en la integración, debe aprenderse de memoria la siguiente ecuación de integración. Y como todas estas ecuaciones también las utiliza la calculadora integral, le ayudará a comprender mejor la estructura del problema y cómo la herramienta lo resuelve.

¡Discutamos las fórmulas ahora!

• 1 dx = x + C

• a dx = ax + C

• x" dx = n+1 + C; n  is not equal to 1

• sin x dx= -cos x + C

• cos x dx = sin x + C

• sec2 x dx = tan x + C

• csc2 x dx = - cot x + C

• sec x(tan x) dx = secx+ C

• fcsc x(cot x) dx = cscx + C

• dx = In |x|+C

Métodos de Integración:

La integración es un término principal. Implica muchos métodos secundarios que pueden ayudarle a navegar a través de la técnica de cálculo, que incluyen:

• Método de descomposición
• Integración por sustitución
• Integración usando fracciones parciales
• Integración por partes

Un vistazo al funcionamiento de la calculadora integral:

Si encuentra la mejor calculadora que se adapta a sus gustos de cálculo, el siguiente paso será cómo puede utilizarla. Permítanos guiarlo de una manera genérica que podría ayudarlo a utilizar la herramienta sin asistencia humana:

• Abra la herramienta en la que más confía
• Selecciona si quieres integrar una integral definida o indefinida
• A continuación, ingresa a la función.
• Ingrese los límites inferior y superior si seleccionó una integral definida
• Toque calcular para obtener sus resultados en el siguiente momento

Características:

• Integración instantánea de la función dada.
• Solución paso a paso para entender mejor el problema
• Interpretación gráfica
• Formas alternativas de integración realizadas por la herramienta.
• Archivos de resultados compartibles y descargables para fines de estudio en grupo

Propiedades de la integración:

Sólo las integrales indefinidas poseen algunas propiedades que son las siguientes:

• ∫ [f(x)±g(x)] dx =∫ f(x) dx ± ∫ g(x) dx
• ∫ k f(x) dx = k ∫ f(x) dx, where k is any real number.
• ∫ f(x) dx = ∫ g(x) dx, if ∫ [f(x)-g(x)] dx = 0

Preguntas frecuentes:

¿Cuáles son las limitaciones de la integración en matemáticas?

Aquí las limitaciones son otro nombre de los límites inferior y superior de la integración que también se pueden resolver con una calculadora integral en un lapso de momentos.

¿Cuál es la principal regla de integración en trigonometría?

• sin y - ∫ sin y dy = - cos y + C
• cos y - ∫ cos y dy = sin y + C
• tan y - ∫ tan y = In (sec y) + C (or) - In I(cos y) + C

¿Por qué necesitamos integración?

En dos dimensiones, la integración se utiliza para determinar el área bajo la región.

En tres dimensiones, la integración se utiliza para determinar el volumen de las funciones u objetos esféricos.

¿Qué funciones no puedes integrar?

Las siguientes funciones nunca podrán integrarse:

• en el intervalo [0, b]; y en cualquier intervalo que contenga 0

La razón principal es que estas funciones contienen un área infinita bajo su gráfica. Incluso una calculadora integral no le dará resultados, ya que va en contra de las leyes de las matemáticas.

¿Es posible la integración de todas las funciones?

No, no se pueden integrar todas las funciones. Por ejemplo, la pregunta anterior respalda la razón.